Type de dimensionnement avec séquences Lucas
La relation entre le texte et le reste d'une page est l'une des caractéristiques clés de tout design.
Le rythme, l'emphase et le ton sont tous compromis sans un type correctement mis à l'échelle. Cependant, la sélection de tailles de texte est souvent une expérience laborieuse et frustrante, sans point de départ standardisé pour nous informer.
Par conséquent, nous trouvons fréquemment des concepteurs Web qui retombent sur les options par défaut présentées par les applications - 8pt, 10pt, 12pt, 14pt, 18pt - faute d’une meilleure solution.
Cette meilleure solution consiste à définir des tailles de type non pas par caprice individuel, mais selon un système prédéterminé; un système simple à utiliser, pratique à mettre en œuvre sur le Web et, surtout, suffisamment flexible pour permettre aux concepteurs d’exprimer toute une gamme d’expressions. Cue: la séquence de Lucas.
Séquences Lucas
La séquence de Fibonacci - enregistrée pour la première fois en Occident au XIIIe siècle par Leonardo Fibonacci - est l'ensemble des entiers suivants (nombres entiers):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ... à l'infini
La séquence a été nommée en l'honneur de Fibonacci par François Édouard Lucas, éminent mathématicien français du XIXe siècle, qui a produit une séquence similaire à celle de Lucas Numbers:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843 ... à l'infini
La séquence de Fibonacci et les nombres de Lucas sont deux variations spécifiques de la séquence Lucas générique.
Les séquences de Lucas et les séquences entières en général ont fait l’objet d’une longue étude pour de nombreux mathématiciens accomplis, nous allons donc résumer le concept comme suit:
- Tout nombre donné dans la séquence est la somme des deux nombres précédents décrits dans cette formule: n = n-1 + n-2
- Les deux premiers chiffres de la séquence - appelés numéros de graine - sont sélectionnés arbitrairement.
Pourquoi utiliser une séquence de Lucas pour définir le type?
Les séquences de Lucas, en particulier sous la forme de la séquence de Fibonacci, sont étroitement liées au rapport d'or, qui se répète dans la nature dans les coquilles, les toiles d'araignées, les formations nuageuses et de nombreuses autres merveilles naturelles. Il existe des preuves solides suggérant que tout ce que nous trouvons attirant visuellement est dû à la relation de cette forme avec le nombre d'or.
Plus important encore, les séquences de Lucas nous fournissent un cadre évolutif pour définir un type à la fois gracieux et rythmé.
Déterminer notre premier numéro de graine
Il y a beaucoup de débats sur la taille correcte du texte du corps pour un site Web. Le 12px reste le plus courant, mais il n’est pas rare de voir de 10 à 16 pixels. Cela est dû en grande partie à un manque de compréhension de ce que les mesures de police signifient réellement. Curieusement, pour ceux d’entre nous qui sont habitués à la normalisation - ou du moins à l’aspiration à la normalisation - il n’existe pas de mesure standard pour la définition de type; deux concepteurs de types différents, dessinant exactement le même design dans un logiciel de production de polices, sont susceptibles de le dessiner à différentes tailles. La variation entre les différentes polices est, sans surprise, trop commune.

La réponse à la question de savoir par où commencer est extrêmement simple. notre taille de texte par défaut sera 1em, ce qui signifie que notre premier numéro de départ sera 1.
L'utilisation de 1em comme point de départ présente un certain nombre d'avantages clés: en tant qu'unité de mesure relative, une em est bien adaptée à la conception réactive; en utilisant ems et multiples de ems, nous pouvons redimensionner notre système en modifiant la taille de la police de base; enfin, il s'agit d'un ajustement conceptuel soigné avec notre séquence de Lucas et qui nous rappellera la séquence entière précise si nous devons revoir la conception plus tard.
Il n'y a rien de mal à utiliser des pourcentages au lieu de ems, ou même de pixels ou de points, mais le em est plus que probable pour l'avenir du web design, nous pouvons donc nous y habituer.
Déterminer notre deuxième numéro de graine
De nombreuses stratégies s’offrent à nous pour déterminer notre deuxième nombre de semences. Certains concepteurs ont une préférence spécifique et choisiraient 1.2em ou similaire. D'autres concepteurs, qui apprécient le mysticisme du Golden Ratio, aimeraient utiliser 1.618em.
Une solution plus pratique consiste à déterminer le deuxième numéro de graine en utilisant la hauteur de ligne du corps du texte. Cependant, étant donné que la hauteur de la ligne est généralement dictée par la longueur de la ligne et que la longueur de la ligne est déterminée par une grille, elle convient mieux à l'impression ou à la conception Web non réactive. Parce que nous nous tournons vers l'avenir et que l'avenir est réactif, cela ne fonctionnera pas pour nous.
Ce qui nous reste, en partie par un processus d'élimination et en partie en raison de son caractère approprié, est la hauteur x du type. Ou plus précisément, la relation entre la hauteur x et le reste du glyphe.
Une caractéristique du bon design est la répétition d'éléments clés, et le fait de porter les proportions du type jusqu'à la page dans son ensemble est une excellente occasion de reconnaître le travail du concepteur de caractères et d'imprégner notre conception du caractère de la police.
Trouver notre hauteur x
Pour trouver la hauteur x de votre police, vous devez ouvrir quelque chose comme Photoshop ou Illustrator et ajouter du texte incluant un ascendeur (par exemple, «d») et la lettre «x». Si vous utilisez un éditeur de bitmap tel que Photoshop, définissez le texte le plus grand possible pour obtenir un résultat précis. Dans ces exemples, j'ai défini la police sur 500pt afin de la mesurer.
Ensuite, mesurez la hauteur entre la ligne d'ascendeur et la ligne de base et la hauteur entre le sommet de x et la ligne de base.
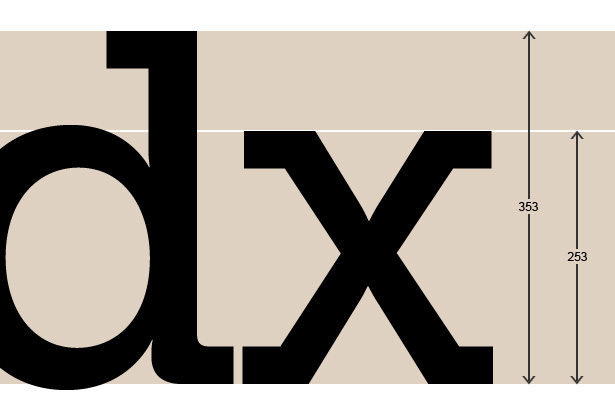
Bien sûr, si vous avez la chance d'avoir accès à un bon logiciel de conception de polices, vous pouvez simplement ouvrir le fichier de polices que vous utiliserez et lire la hauteur et la hauteur de l'ascenseur.
Divisez maintenant la hauteur x par la hauteur de l'ascendeur pour trouver la hauteur x en pourcentage de l'ensemble:
hauteur x / hauteur de l'ascendeur * 100 = numéro de la deuxième graine
Dans le cas de la police dans l'exemple (qui est Museo Slab), le résultat est le suivant:
253/353 = 0.71671388
ou 0.716em
Pourquoi ne mesurons-nous pas du haut de l'ascendeur au bas du descendeur? Parce que les caractères n'ont pas tendance à avoir à la fois un ascendeur et un descendant (une exception occasionnelle étant la lettre «f») et que les relations entre les formes qui composent la conception de la police sont basées sur la relation entre la hauteur x et une tige plus longue. Il est possible de mesurer le descendant à la place, mais comme la hauteur du cap (la hauteur des chapiteaux) est généralement très proche de l'ascendeur, c'est ma préférence. Si vous utilisez une police avec une qualité plus dominante - le contraste dans l’épaisseur de différents traits, par exemple -, vous pouvez utiliser cette valeur à la place du rapport ascendeur / hauteur x.
La détermination de la manière d’arriver à votre deuxième numéro de départ est l’une des principales décisions à prendre en matière de conception, mais ce n’est pas une tâche difficile. Choisissez un numéro sur un chapeau si vous préférez, et continuez, les bonnes choses sont à venir.
Il est intéressant de noter que si vous modifiez l'équation et divisez la hauteur de l'ascendeur par la hauteur x, vous obtiendrez un nombre supérieur à un. Dans ce cas, votre séquence sera plus raide et un peu plus dramatique.
Créer notre séquence
Nous avons donc nos deux nombres de base: 1em et 0.716em et nous avons la formule n = n-1 + n-2:
1 + 0.716 = 1.716
0,716 + 1,716 = 2,432
1.716 + 2.432 = 4.148
etc.
Ce qui se traduit par la séquence suivante:
1, 0,716, 1,716, 2,432, 4,148, 6,58, 10,728, 17,308, 28,036 ... à l'infini
Le bit de conception
Jusqu'à présent, nous avons choisi des mathématiques de base, mais utiles, et nous sommes arrivés à une séquence qui nous donne une gamme de tailles allant de 1em à 28.036em et au-delà si nécessaire.
Nous pouvons maintenant utiliser ces valeurs en tant que tailles de type de manière séquentielle pour créer un schéma de type bien proportionné:

Vous remarquerez que nous commençons avec p mis à 0.716 et h4 à 1, bien que cela ne soit pas séquentiellement correct. La raison en est que, en termes de hiérarchie, h4 est plus important que p. Notre séquence de Lucas ne doit pas dicter la hiérarchie sur la page, elle dicte les relations d'échelle des différents éléments. Seul votre contenu peut dicter la hiérarchie .
Comme nous ne sommes pas limités à des valeurs consécutives dans notre séquence et que nous sommes en mesure de choisir les entiers que nous utilisons, nous obtenons toujours un rythme et une structure avec la même séquence. Même si nous adoptons une approche très dramatique:

La même séquence de Lucas peut également être utilisée pour créer un schéma professionnel plus réservé:

L’essence de ce système est que les relations d’échelle sont maintenues, que la hiérarchie est proportionnée, mais que le concepteur dispose d’une grande diversité. C'est là que vous devez gagner votre argent: en sélectionnant les tailles sur la balance pour créer une hiérarchie et une emphase.
La flexibilité
Souvent, la taille du type est dictée par plus que l'accent: les problèmes d'accessibilité se posent si nous parlons d'un public ayant des difficultés visuelles; le volume même du contenu peut créer des restrictions; nous devrons peut-être faire preuve de souplesse - littéralement - lors de la conception d'une disposition fluide.
Heureusement, CSS gère cette situation avec facilité. Comme nous utilisons ems pour nos tailles, nous pouvons configurer notre type en utilisant notre séquence Lucas, puis mettre à l'échelle le tout en définissant une taille par défaut sur la balise body, en conservant le rythme de notre conception, mais en augmentant ou en diminuant les valeurs réelles.

Notez dans cette image que les tailles p, h2 et h1 restent les mêmes, toutes tirées de notre séquence. C'est la variation de la taille de la police de la balise body (0.8em à gauche et 1.4em à droite) qui descend en cascade, créant des résultats radicalement différents.
finalement
Aussi dépendant des mathématiques sous-jacentes que ce système, il est important de reconnaître que la conception ne peut être réduite à un ensemble d’équations. Cette méthode de type de dimensionnement vous donne une structure avec laquelle travailler, et vous aidera à créer des schémas de types bien proportionnés, mais il vous appartient, en tant que concepteur, d’utiliser le système comme un outil et non comme une béquille.
Les notes et les échelles de la musique, même le jazz, peuvent être réduites à un ensemble d’équations décrivant leur relation, mais il faut que quelqu'un comme John Coltrane donne vie à ces relations.